Khi nhắc đến những thuật toán được sử dụng phổ biến trong lập trình thì không thể nào thiếu Quick Sort. Cũng giống như các thuật toán khác, Quick Sort không hề dễ “xơi” mà cần có thời gian nghiên cứu kỹ lưỡng để hoàn toàn nắm chắc nó trong bàn tay. Trong bài viết sau, Teky sẽ giúp bạn giải đáp một số khái niệm cơ bản xung quanh thuật toán Quick Sort. Đây là sẽ những kiến thức hữu ích mà bất kỳ lập trình viên nào cũng cần hiểu rõ.
Tìm hiểu thuật toán Quick Sort là gì?
Giới thiệu về thuật toán sắp xếp
Vì Quick Sort cũng là một dạng thuật toán sắp xếp nên đầu tiên chúng ta sẽ điểm nhanh qua các phân loại phổ biến.
- Thuật toán đơn giản với độ phức tạp O(n^2) bao gồm: Insertion Sort (sắp xếp chèn), Bubble Sort (sắp xếp nổi bọt), Selection Sort (sắp xếp lựa chọn).
- Thuật toán hiệu quả với độ phức tạp O(nlogn) bao gồm: Heap Sort (sắp xếp vun đống), Merge Sort (sắp xếp trộn), Quick Sort (sắp xếp nhanh).
- Thuật toán đặc biệt với độ phức tạp O(n) bao gồm: Counting Sort (sắp xếp đếm), Bucket Sort (sắp xếp phân cụm), Radix Sort (sắp xếp cơ số).
- Xử lý các tập dữ liệu lớn bao gồm: External sort (sắp xếp ngoài).
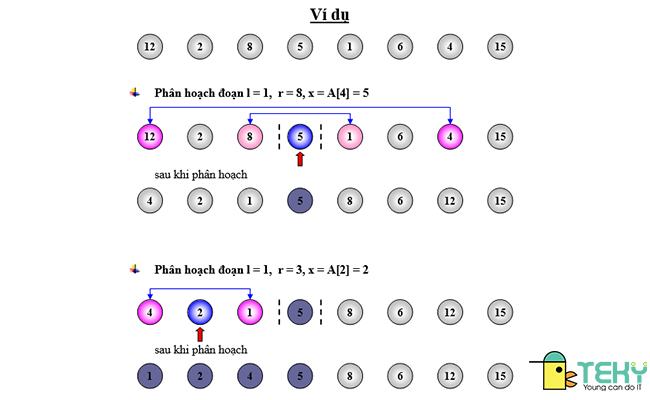
Một ví dụ về thuật toán Quicksort Java
Thuật toán sắp xếp trong dùng để xử lý các tệp dữ liệu nhỏ. Họ dữ liệu sẽ được đưa toàn bộ vào trong bộ nhớ của máy tính. Còn thuật toán sắp xếp ngoài chỉ sử dụng được cho các tệp dữ liệu lớn. Họ dữ liệu không thể đưa toàn bộ dữ liệu vào bộ nhớ trong cùng một lúc nhưng có thể đọc lần lượt từng bộ phận tại bộ nhớ ngoài.
Khái niệm thuật toán Quick Sort
Quick Sort có khái niệm khá tương đồng với Merge Sort. Tức là đều hoạt động dựa trên cơ chế chia và trị. Nó sẽ chịu trách nhiệm phân chia dữ liệu thành các mảng nhỏ và sắp xếp một cách nhanh chóng. Đó cũng là lý do tại sao Quick Sort mang ý nghĩa là sắp xếp nhanh.
Quick Sort được chia vào phân loại giải thuật sắp xếp với phức tạp thời gian là trung bình O(n log n) và xấu nhất O(n2). Độ phức tạp dữ liệu của thuật toán QuickSort tùy thuộc vào cách hiện thực. Tần suất tối ưu là thỉnh thoảng.
Thuật sắp xếp nhanh Quick Sort sẽ tiến hành chia nhỏ mảng thành hai phần. Thông qua phương pháp so sánh từng phần tử với một phần tử chốt, ta sẽ thu được một mảng gồm những phần tử nhỏ hơn hoặc bằng phần tử chốt và một mảng gồm những phần tử lớn hơn phần tử chốt. Mỗi phiên bản Quick Sort C++ khác nhau sẽ có một cách chọn phần tử chốt khác nhau. Có thể là phần tử đầu tiên, cuối cùng hoặc phần tử ngẫu nhiên, phần tử trung vị.
Hoạt động phân chia này diễn ra liên tục và chỉ dừng lại khi độ dài của mỗi phần tử con bằng 1. Để sắp xếp nhanh các phần tử con thu được thành một mảng hoàn chỉnh, người dùng sẽ sử dụng phương pháp đệ quy. Tất cả các thao tác này đều diễn ra trong thời gian tuyến tính.
Ý tưởng của thuật toán Quick Sort
Cách triển khai thuật toán Quick Sort Java
Đầu tiên, ta sẽ tiến hành chọn một pivot. Về cách chọn pivot, có rất nhiều cách để dùng trong nhiều trường hợp khác nhau. Tuy nhiên phổ biến nhất là chọn pivot đầu, pivot cuối và pivot giữa.
Sau khi đã chọn được phần tử người dùng sẽ cần khai báo 2 biến của 2 con trỏ để duyệt 2 phía của phần tử pivot. Lần lượt, ta sẽ trỏ biến bên trái đến mỗi phần tử nằm bên trái của phần tử pivot. Ngược lại, ta cũng sẽ trỏ biến bên phải đến mỗi phần tử nằm bên phải của phần tử pivot.

Ý tưởng về thuật toán Quicksort trong C++
Với mỗi lần trỏ như vậy, ta tiến hành phân loại các phần tử. Tại bên trái, nếu biến trỏ nhỏ hơn phần tử thì chuyển giá trị sang phải. Còn tại bên phải, nếu biến trỏ nhỏ hơn phần tử thì chuyển giá trị sang trái. Nếu biến trỏ bằng phần tử thì tráo đổi giá trị 2 bên phải và trái. Cuối cùng, khi tất cả phần tử trái lớn hơn phần tử phải thì đây chính là giá trị chốt mới.
Lý thuyết cơ bản là như vậy nhưng với mỗi cách chọn phần tử, quá trình triển khai sẽ khác nhau. Dưới đây là ví dụ về 3 cách chọn phần tử phổ biến nhất.
Cách 1: Chọn phần tử đầu trong thuật toán Quick Sort
quickSort = (unSortedArr) => {
// nếu mảng không quá 1 phần tử thì mảng đó đã được sản xuất
if (unSortedArr.length < 2) return unSortedArr;
const pivot = unSortedArr[0]; //lấy phần tử đầu của mảng làm phần tử chốt
const leftArr = []; // mảng chứa phần tử nhỏ hơn pivot
const rightArr = []; // mảng chứa phần tử lớn hơn pivot
let currentItem; // phần tử đang được xét
// loop các phần tử còn lại trong mảng trừ phần tử chốt.
// Do pivot là ptu đầu tiên nên i sẽ bắt đầu từ 1
for (let i = 1; i < unSortedArr.length; i++) {
currentItem = unSortedArr[i];
if (currentItem < pivot) {
leftArr.push(currentItem);
} else {
rightArr.push(currentItem);
}
}
return […this.quickSort(leftArr), pivot, …this.quickSort(rightArr)];
}
Cách 2: Chọn phần tử cuối
quickSort = (unSortedArr) => {
if (unSortedArr.length < 2) return unSortedArr;
const pivot = unSortedArr[unSortedArr.length – 1]; //phần tử cuối mảng làm chốt
const leftArr = [];
const rightArr = [];
let currentItem;
// Do pivot là ptu cuối nên length sẽ trừ đi 1
for (let i = 0; i < unSortedArr.length – 1; i++) {
currentItem = unSortedArr[i];
if (currentItem < pivot) {
leftArr.push(currentItem);
} else {
rightArr.push(currentItem);
}
}
return […this.quickSort(leftArr), pivot, …this.quickSort(rightArr)];
}
Cách 3: Chọn phần tử giữa trong thuật toán Quick Sort
quickSort = (unSortedArr) => {
if (unSortedArr.length < 2) return unSortedArr;
// lấy phần tử giữa làm chốt
const pivotIndex = Math.floor(unSortedArr.length / 2);
const pivot = unSortedArr[pivotIndex];
const leftArr = [];
const rightArr = [];
let currentItem;
unSortedArr.splice(pivotIndex, 1); // loại bỏ ptu pivot trong mảng
for (let i = 0; i < unSortedArr.length; i++) {
currentItem = unSortedArr[i];
if (currentItem < pivot) {
leftArr.push(currentItem);
} else {
rightArr.push(currentItem);
}
}
return […this.quickSort(leftArr), pivot, …this.quickSort(rightArr)];
}
Giải thuật toán Quick Sort

Các bước trong thuật toán Quicksort không hề khó như bạn tưởng
Dưới đây là một ví dụ về quá trình giải thuật toán Quicksort C++ được viết bằng ngôn ngữ lập trình Java:
public class QuickSort {
public static void main(String[] args) {
int[] x = {6, 2, 3, 4, 5, 9, 1};
printArray(x);
int left = 0;
int right = x.length – 1;
quickSort(x, left, right);
printArray(x);
}
public static void quickSort(int[] arr, int left, int right) {
if (arr == null || arr.length == 0)
return;
if (left >= right)
return;
int middle = left + (right – left) / 2;
int pivot = arr[middle];
int i = left, j = right;
while (i <= j) {
while (arr[i] < pivot) {
i++;
}
while (arr[j] > pivot) {
j–;
}
if (i <= j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j–;
}
}
if (left < j)
quickSort(arr, left, j);
if (right > i)
quickSort(arr, i, right);
}
public static void printArray(int[] arr) {
for(int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ” “);
}
System.out.println();
}
}
Độ phức tạp của thuật toán sắp xếp nhanh
Công thức tính thời gian của thuật toán Quick Sort được viết như sau:
T(n) = T(k) + T(n-k-1) + θ(n)
Trong đó, T(k) và T(n-k-1) thời gian dành cho hai cuộc gọi đệ quy. Còn θ(n) là tiến trình phân vùng. k là số phần tử nhỏ hơn phần tử chốt. Thời gian của thuật toán Quick Sort còn phụ thuộc vào mảng đầu và chiến lược chia mảng.
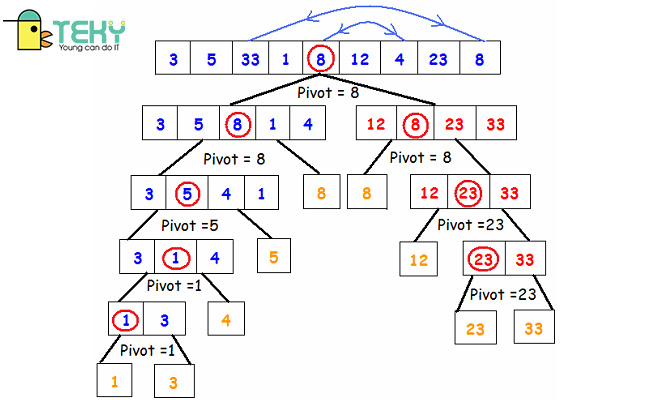
Cách triển khai thuật toán Quick Sort
- Với phân đoạn không cân bằng: Khi trường hợp xấu nhất xảy ra (pivot là phần tử đầu và dãy đã được sắp xếp nhanh), độ phức tạp của thuật toán Quick Sort sẽ là O(n^2). Tại thời điểm đó, mảng không được chia thành bất kỳ phần nào cả, 2 bài toán con lần lượt có kích thước là n-1 và 0.
- Với phân đoạn hoàn hảo: Mỗi bài toán con có kích thước là n/2. Mảng cũng được phân thành hai phần bằng nhau. Độ phức tạp lúc này là O(nlogn).
- Với phân đoạn cân bằng: Một bài toán con có kích thước là n-k, bài còn lại có kích thước là k. Độ phức tạp lúc này là O(n).
Mời bạn đọc tham khảo thêm: Wireframe là gì?
Kết luận
Thông qua bài viết trên, Teky đã giúp bạn đọc hiểu thêm về thuật toán Quick Sort trong Java. Mong rằng bạn đọc đã nắm rõ được những thông tin cơ bản xoay quanh thuật toán này. Chúc bạn nhanh chóng ứng dụng được Quicksort Java vào trong công việc của mình.
The post Thuật toán Quick Sort là gì? Giới thiệu lập trình chi tiết nhất appeared first on TEKY - Học viện sáng tạo công nghệ.
source https://teky.edu.vn/blog/thuat-toan-quick-sort/
Không có nhận xét nào:
Đăng nhận xét